-
Scam Alert. Members are reminded to NOT send money to buy anything. Don't buy things remote and have it shipped - go get it yourself, pay in person, and take your equipment with you. Scammers have burned people on this forum. Urgency, secrecy, excuses, selling for friend, newish members, FUD, are RED FLAGS. A video conference call is not adequate assurance. Face to face interactions are required. Please report suspicions to the forum admins. Stay Safe - anyone can get scammed.
-
Several Regions have held meetups already, but others are being planned or are evaluating the interest. The Calgary Area Meetup is set for Saturday July 12th at 10am. The signup thread is here! Arbutus has also explored interest in a Fraser Valley meetup but it seems members either missed his thread or had other plans. Let him know if you are interested in a meetup later in the year by posting here! Slowpoke is trying to pull together an Ottawa area meetup later this summer. No date has been selected yet, so let him know if you are interested here! We are not aware of any other meetups being planned this year. If you are interested in doing something in your area, let everyone know and make it happen! Meetups are a great way to make new machining friends and get hands on help in your area. Don’t be shy, sign up and come, or plan your own meetup!
You are using an out of date browser. It may not display this or other websites correctly.
You should upgrade or use an alternative browser.
You should upgrade or use an alternative browser.
Help my decroded brain with some math
- Thread starter DPittman
- Start date
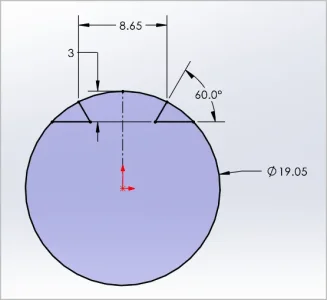
If I honor the 3mm, the distance across the corners is 9.53mm
If I honor the 3mm, the distance across the corners is 9.53mm
Don't both of these results assume that the 60 degree dovetail ends up tangent to the circumference?
As far as I know, that isn't really a requirement.
The only reliable way is measure using pins because corners are burred or chamfered or whatever. If you tell me the wire diameter & outer distance combination (example 3mm & 13.06mm) that becomes the constraint & I can tell you the rest of the corresponding dimensions which result.
Absolutely. In fact, that's why I was happy that @thestelster had volunteered to do the math. That left me the easy work of suggesting wires. If the angles are right, the wires always work.
@DPittman - as Peter has shown, the math is absolute but the measurements that go with the math are subject to many errors because of variables like chamfers, burrs, dovetail root, etc. Without reliable measurements, the math can't be reliably used.
The wires almost always work. So I use wires or rods or gauge pins to get a good repeatable reliable result.
One of your other measurements can also be improved with wires. Assuming they sit proud of the barrel OD between them, you can get the true height by measuring across both wires to the opposite side, and then subtracting the OD of the wires and comparing that to the OD of the barrel.
Somebody has to double check my math please.
It looks good to me Stel. Kudos to you for taking that on. That was the hard part if you ask me!
Success!
I see you posted your results while I was commenting.
Well done!
Don't both of these results assume that the 60 degree dovetail ends up tangent to the circumference?
As far as I know, that isn't really a requirement.
No, the dovetail ends are not tangent, only coincident. I have only defined their angle. But I thought something looked fishy. Disregard my first 2 pics, this is the correct. Black means fully defined, blue means still somewhat unconstrained. Grey means a resultant dimension at any desired orientation. I think must have inadvertently turned on self-mirroring & it applied another constraint.
Left, dovetails can float in size & position until some other dimension is applied
Center, I defined HZ dimension = 8.65, now fully defined
Right, defined a different HZ dimension, again now fully defined
By putting gage pins in & defining that distance it would be the same as center & right
Attachments
No, the dovetail ends are not tangent, only coincident.
Sorry, I did say that wrong. What I should have said is "Don't both of these results assume that the 60 degree dovetail ends up intersecting the OD at a point that is perpendicular to the tangent of the circumference?" I suppose I could have also said perpendicular to the circumference but that's only for a single point.
Fundamentally, I wasn't arguing that your point was incorrect. It was and still is valid. Only that the calculation wasn't strictly correct.
Either way, you still need wires.
For all of these reasons, the depth measurement should be more reliable than the width. A real part will have to have the corners chamfered / rounded and have some slop.
The most important practical consideration is how far to cut in from each side. That's a number that can be directly used on the mill
The angles might or might not be perpendicular to the tangents at the points that they intersect, but I think that's somewhat irrelevant. For the same angle and horizontal cut, a deeper one will increase the angle, and a shallower one will decreases it (reverse this if you are thinking of the opposite angle). A good design will have them very close to perpendicular to the tangent because that optimizes stress in the material, but there is no accounting for a bad design
If you have a reliable measurement of the depth, and you are confident about the angle, then It is easy to know how far to cut from the perpendicular at the top of the cut. But that's probably a hard spot to locate. The bottom of the cut seems easier to find. That means that what you really want is the sum of the horizontal portions of two triangles - both of which you can find from Pythogous

The most important practical consideration is how far to cut in from each side. That's a number that can be directly used on the mill
The angles might or might not be perpendicular to the tangents at the points that they intersect, but I think that's somewhat irrelevant. For the same angle and horizontal cut, a deeper one will increase the angle, and a shallower one will decreases it (reverse this if you are thinking of the opposite angle). A good design will have them very close to perpendicular to the tangent because that optimizes stress in the material, but there is no accounting for a bad design
If you have a reliable measurement of the depth, and you are confident about the angle, then It is easy to know how far to cut from the perpendicular at the top of the cut. But that's probably a hard spot to locate. The bottom of the cut seems easier to find. That means that what you really want is the sum of the horizontal portions of two triangles - both of which you can find from Pythogous
DPittman
Ultra Member
Did your see mine!? Now that was bad.My drawing is very bad,